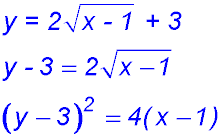Functs - domain & range TYS 1 Solns

For each of the questions in the following table,
determine both the domain and the range of the function
unless otherwise indicated.

Linear

1. 2x + 3y = 6

The x and y values can extend in both directions without limit. Hence:

Domain (-∞, ∞)
Range (-∞, ∞)

2. For y = 3, the x values can extend in both directions but the y value is always = 3. Hence:

Domain (-∞, ∞)
Range [3, 3].

3. For x = 2, the y values can extend in both directions but the x value is always = 2. Hence:

Domain [2, 2]
Range (-∞, ∞).

4. For y = -14x, the x and y values can extend in both directions without limit. Hence:

Domain (-∞, ∞)
Range (-∞, ∞).

Quadratic

5. .

If x becomes greater than 5, the term under the square root becomes less than zero and so we cannot take the square root. But x can take any negative value.

The minimum value for y is zero and this occurs when
x = 5. Hence:

Domain [0, 5]
Range [0, ∞).

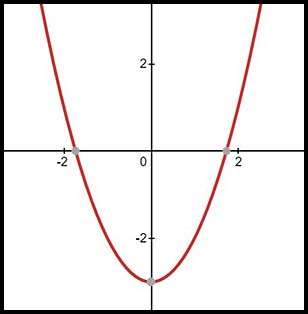
6. y = 5 - x²

The equation describes an upside down parabola with a vertex at (0, 5).

Hence x values can extend
from - infinity to + infinity.

y values can extend from and equal to 5 down to - infinity.

∴ Domain: (-∞, ∞)

Range: (-∞, 5]

7. y = x² - 3

The equation describes a parabola with a vertex at (0, -3).

Hence x values can extend
from - infinity to + infinity.

y values can extend from and equal to -3 up to infinity.

∴ Domain: (-∞, ∞)

Range: [-3, ∞)

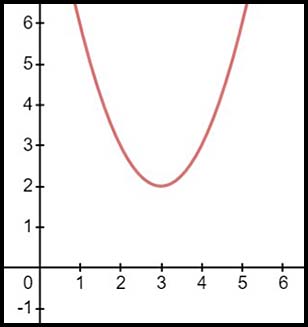
8. y = (x - 3)² + 2

The equation describes a parabola with a vertex at (3, -2).

Hence x values can extend
from - infinity to + infinity.

y values can extend from and equal to +2 up to infinity.

∴ Domain: (-∞, ∞)

Range: [2, ∞)

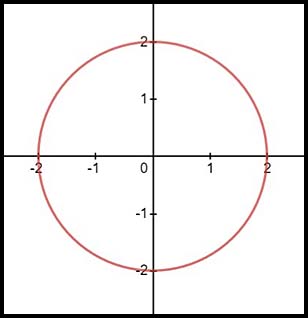
Other basic combinations.

9. x² + y² = 4?

The equation describes a circle with centre at (0, 0) and radius of 2.

Hence x values can extend
from (and including) - 2 to + 2.

y values can extend from (and including) -2 to +2.

∴ Domain: [-2, 2]

Range: [-2, 2]

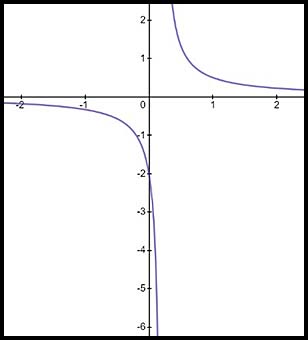
10.

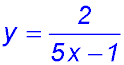
The equation describes a hyperbola with a vertical asymptote at x = 0.2 and a horizontal asymotote at y = 0.

Hence x values can extend
from - infinity to + infinity except at x = 0.2.

y values can extend from
- infinity to + infinity except
at y = 0.

Hence each has to be written as a combination of two parts:

∴ Domain:
(-∞, 0.2) ∪ (0.2, ∞)

Range: (-∞, 0) ∪ (0, ∞)

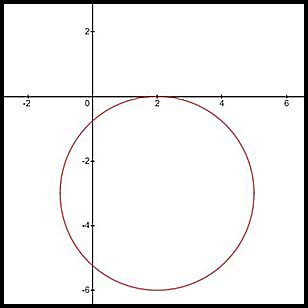
11.

The equation describes a circle with centre at (2, -3) and
a radius of 3.

Hence x values can extend
from (and including) - 1 to 5.

y values can extend from (and including) -6 to 0.

∴ Domain: [-1, 5]

Range: [-6, 0]

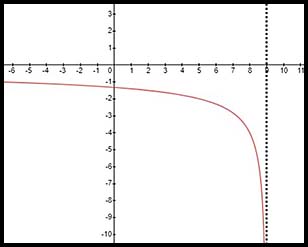
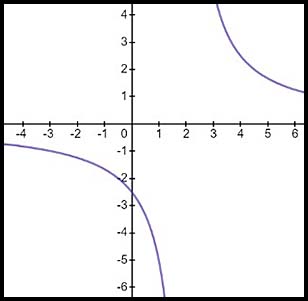
12.

The equation describes a hyperbola with a vertical asymptote at x = 2 and a horizontal asymotote at y = 0.

Hence x values can extend
from - infinity to + infinity except at x = 2.

y values can extend from
- infinity to + infinity except
at y = 0.

Hence each has to be written as a combination of two parts:

∴ Domain:
(-∞, 2) ∪ (2, ∞)

Range: (-∞, 0) ∪ (0, ∞)

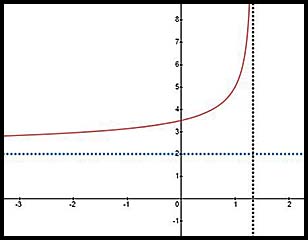
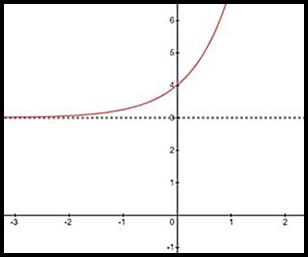
13.

The equation describes an exponential curve with a horizontal asymptote at x = 3.

Hence x values can extend
from -∞ to +∞.

y values can extend from 3 (but not = 3) to +∞.

∴ Domain: (-∞, +∞)

Range: (3, ∞)

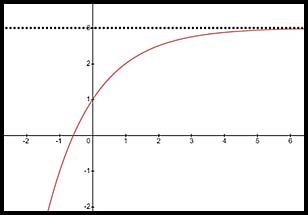
14.

The equation describes an exponential curve with a horizontal asymptote at y = 3.

Hence x values can extend
from -∞ to +∞.

y values can extend from -∞ up to but not including +3.

∴ Domain: (-∞, +∞)

Range: (-∞, 3)

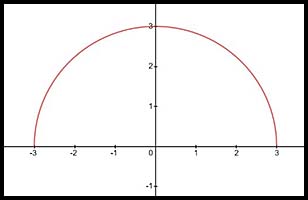
Radicals - one term

15.

The equation describes the upper half of a circle with centre at (the origin and radius of 3.

Hence x values can extend
from -3 to +3 (inclusive).

y values can extend from 0 to +3.

∴ Domain: [-3, +3]

Range: (3, ∞)

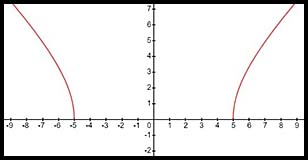
16.

The equation describes a special type of hyperbola (one outside your syllabus). It has two arcs above the x axis branching away from the axis of symmetry.

Hence x values can extend
from - infinity to -3 and from +3 to + infinity.

y values can extend from 0 to +infinity.

∴ Domain:
(-∞, -3] ∪ [3, ∞)

Range: [0, ∞)

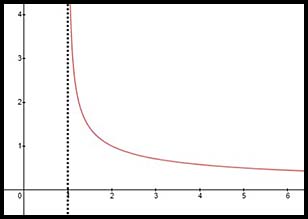
17. .

The equation does not describe one of the common curves. It is confined to the positive quadrant. The denominator cannot = 0 so there is a vertical asymptote
at x = 1.

Hence x values can extend
from 1 to +infinity.

y values can extend from 0 to +infinity.

∴ Domain: (1, ∞)

Range: (0, ∞)

18. .

The equation does not describe one of the common curves. It is confined to the region below the x axis (because of the negative sign) and to the left of the asymptote at
x = 3. The denominator cannot = 0 so the vertical asymptote is at at
x = 3.

Hence x values can extend
from -infinity to 3.

y values can extend from -infinity to y = 0 (the x axis).

∴ Domain: (-∞, 3)

Range: (-∞, 0)

Two terms

19.

The equation describes a sideways parabola. It is confined to the positive quadrant with the vertex at (1, 3) - see the following change to the way the equation is written.

Hence x values can extend
from 1 to +infinity.

y values can extend from 3 to +infinity.

∴ Domain: [1, ∞)

Range: [3, ∞)

20.

The equation does not describe one of the common curves. It is better to approach determining domain and range algebraically:

It is not possible for x = 4/3 because then the denominator equals zero. So there is an asymptote at that value. x cannot take a value greater than 4/3 because then the term under the square root is negative.

When x = 0, y = 3.5.

When x approaches a large negative number, the denominator becomes large and hence the fraction approaches zero. Then g(x) approaches 2.

Hence x values extend
from -infinity to 4/3 = 1.33...

y values extend from 2 to +infinity.

∴ Domain: (-∞, 1.3)

Range: (2, ∞)

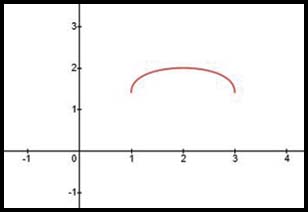
21.

The equation does not describe one of the common curves. It is better to approach determining domain and range algebraically:

In the first term, x cannot be less than 1. In the second term, x cannot exceed 3. Hence x values can equal 1 or 3 or somewhere in between.

When x = 1 or 3, one of the two terms = 0 and f(x) = √2.

f(2) = √1 + √1 = 2.

Hence x values extend from
and = 1 to 3.

y values extend from and = √2 to 2.

∴ Domain: [1, 3]

Range: [√2, 2]

22.

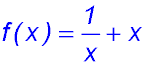
Remember the question asks for domain and range - not to draw this unusual graph (unless you want to for yourself).

Approach the equation algebraically:

Clearly the function is odd and so the graph is symmetrical about the origin.

The first term shows x cannot = 0.

When x approaches 0 from above, the first term approaches +inf. The converse also applies.

The second term shows that x can be any number and as x increases, f(x) increases linearly.

Now try some other numbers. - say x = ±1.
f(1) - 2 and f(-1) = -2.

With x between 0 and 1, f(x) is larger than 2 because of the reciprocal.

Hence x values extend from -∞ to +∞
but ≠ 0.

y values extend from -∞ up to -2 and then from +2 upwards.

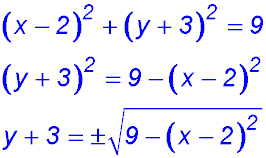
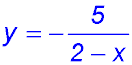
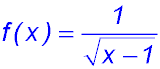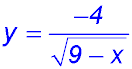∴ Domain: (-∞, 0) ∪ (0, ∞)

Range: (∞, 2] ∪ {2, ∞)